Чему равна общая депрессия параллельного соединения
Чему равна общая депрессия параллельного соединения
Параллельное и последовательное соединение выработок
Рассмотрим часть вентиляционной схемы на рис. 5.1 от точки 2 до точки 9: от воздухоподающего ствола воздух поступает по откаточному квершлагу 2-3 и этот путь можно выразить в виде безразмерной линии 2-3 на рис. 5.2 (а). Далее (см. рис. 5.1) поток воздуха раздваивается и идет по промежуточным штрекам 3-4 и 3-6, которые также можно выразить безразмерными линиями 3-4 и 3-6 на рис. 5.2 (а). Пройдя очистные забои 4-5 и 6-7, а также вентиляционные штреки 5-8 и 7-8, потоки в точке 8 сливаются и общим потоком движутся по вентиляционному квершлагу 8-9 к вентиляционному стволу, что можно выразить в виде графического изображения на рис. 5.2 (а).
Безразмерное произвольное графическое изображение части схемы вентиляции на рис. 5.2 (а) называется уже вентиляционной сетью. Точки, в которых сходятся выработки называются узлами, а сами выработки – ветвями.
Часть вентиляционной сети на рис. 5.2 (а) можно изобразить в виде прямой, включающей промежуточный штрек 3-4, к концу которого подсоединено начало очистного забоя 4-5, а далее к концу забоя – начало вентиляционного штрека 5-8 (рис. 5.2, б). Такое соединение (рис. 5.2, б), когда к концу предыдущей ветви подсоединяется начало следующей, называется последовательным.
Общее сопротивление последовательного соединения равно арифметической сумме сопротивлений выработок (ветвей), т.е.
 , (5.1)
, (5.1)
где n – количество ветвей в соединении.
 Рис. 5.2 Последовательное (б) и параллельные (а, в, г) соединения горных выработок Рис. 5.2 Последовательное (б) и параллельные (а, в, г) соединения горных выработок |
ПРИМЕР РАСЧЕТА 1.
Определить сопротивление соединения 3-8 при известных 
 и
и  даПа×с 2 /м 6 .
даПа×с 2 /м 6 .
Решение:  0,00454 + 0,00700 + 0,010234 = 0,021774 даПа×с 2 /м 6 .
0,00454 + 0,00700 + 0,010234 = 0,021774 даПа×с 2 /м 6 .
Точно таким же образом можно определить сопротивление последовательного соединения 3-6-7-8, используя формулу (5.1). Пусть это сопротивление равно:  даПа×с 2 /м 6 .
даПа×с 2 /м 6 .
Упростим вентиляционную сеть на рис. 5.2 (а), заменив последовательные соединения в виде одной ветви с суммарным значением сопротивления, т.е.  и
и  . Тогда получаем сеть на рис. 5.2 (в), в которой начала ветвей соединены в одной точке, а концы – в другой. Такое соединение называется параллельным.
. Тогда получаем сеть на рис. 5.2 (в), в которой начала ветвей соединены в одной точке, а концы – в другой. Такое соединение называется параллельным.
На рис. 5.2 (в) показано простое параллельное соединение. Если в соединении три и более ветвей, оно называется сложным параллельным соединением – рис. 5.2 (г).
Аэродинамическое сопротивление простого параллельного соединения подсчитывается по формулам
 или
или 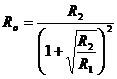 . (5.2)
. (5.2)
Аэродинамическое сопротивление сложного на рис. 5.2 (г) параллельного соединения подсчитывается по формулам, которые, имея разный вид, дают одно и то же значение
 или
или  . (5.3)
. (5.3)
Если к простому параллельному соединению подается объем воздуха, равный Q, то этот объем распределяется в ветвях пропорционально их сопротивлениям
 и
и  (5.4)
(5.4)
для сложного параллельного соединения:
 ,
,  и т.д. (5.5)
и т.д. (5.5)
ПРИМЕР РАСЧЕТА 2..
а. Определить сопротивление простого параллельного соединения при известных сопротивлениях ветвей  и
и  (см. данные в примере расчета 1). По формуле (5.2) имеем:
(см. данные в примере расчета 1). По формуле (5.2) имеем: 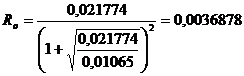 даПа×с 2 /м 6 .
даПа×с 2 /м 6 .
б. Определить сопротивление простого параллельного соединения, если  даПа×с 2 /м 6 :
даПа×с 2 /м 6 :  даПа×с 2 /м 6 .
даПа×с 2 /м 6 .
в. Определить сопротивление сложного параллельного соединения из 5 ветвей, имеющих равные аэродинамические сопротивления  даПа×с 2 /м 6 .
даПа×с 2 /м 6 .
На основании б)  даПа×с 2 /м 6 . Из приведенных расчетов очевидно, что сопротивление сложного параллельного соединения, состоящего из n ветвей с равными сопротивлениями, равно
даПа×с 2 /м 6 . Из приведенных расчетов очевидно, что сопротивление сложного параллельного соединения, состоящего из n ветвей с равными сопротивлениями, равно  .
.
Дата добавления: 2018-04-15 ; просмотров: 636 ; Мы поможем в написании вашей работы!
Виды вентиляционных соединений горных выработок
Последовательное соединение. Соединение выработок без разветвлений называется последовательным. Например, выемочный участок состоит из конвейерного штрека (1-2), лавы (2-3) и вентиляционного штрека 3-4 (рис. 4).
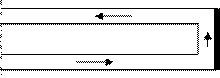 |
Рис. 4 Упрощенная схема выемочного участка
направление движения воздуха

Депрессия последовательного соединения определяется как сумма депрессий входящих в него ветвей (рис.4)
Общее сопротивление последовательного соединения равно сумме сопротивлений отдельных выработок составляющих его (см. рис.4)
Расход воздуха во всех выработках одинаков Qобщ = Q1-2 = Q2-3 = Q3-4 .
Тогда, умножив все члены уравнения (21) на Q 2 , получим
Депрессия последовательного соединения равна сумме депрессий, входящих в него ветвей.
Параллельное соединение.Параллельным соединением выработок называется такое соединение, когда выработки связаны между собой только в двух общих узлах.
Пример простого параллельного соединения показанна рис.5. В параллельном соединении разность давлений (депрессия) в узлах для всех ветвей одинакова. Для схемы представленной на рис.5 можно записать, что общая депрессия параллельного соединения равна депрессии любой из его ветвей
 |


Рис.5 Простое параллельное соединение
Общий расход воздуха в параллельном соединении равен сумме расходов в отдельных ветвях
Подставляя вместо расходов воздуха, в уравнении (13) соотношение  , с учетом (24) можно записать формулу для определения общего сопротивления параллельного соединения
, с учетом (24) можно записать формулу для определения общего сопротивления параллельного соединения
 . (14)
. (14)
или в общем виде
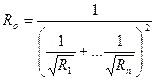 . (15)
. (15)
В частном случае, когда R1= R2 =…= Rn можно записать
 . (16)
. (16)
Расход воздуха в одной из ветвей (Q1) параллельного соединения (из двух ветвей), можно определить через общий расход воздуха
Q1 =  . (17)
. (17)
Распределение воздуха, в ветвях параллельного соединения, происходит обратно пропорционально корню квадратному из отношения сопротивлений ветвей.
Диагональное соединение.Диагональное соединение можно рассматривать, условно, как параллельное соединение двух выработок, связанных между собой выработкой-диагональю (рис.6, участок ВС).
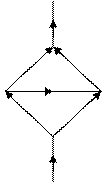
Рис.6 Схема диагонального соединения
Основным свойством диагонального соединения является то, что движение воздуха в ветви-диагонали не зависит от ее аэродинамического сопротивления. Так, например воздух будет двигаться из узла В в узел С если выполняется условие
 . (18)
. (18)
При равенстве этих отношений
 ,
,
расход воздуха в диагонали равен нулю (QВС = 0).
Депрессия диагонального соединения равна сумме депрессий выработок последовательно примыкающих друг к другу
Общее сопротивление диагонального соединение определяет формула
где Q0 – расход воздуха, проходящий через диагональное соединение.
Расчет воздуха в ветвях диагонального соединения определяется по приближенным формулам с использованием уравнения гиперболы.
Сложные (комбинированные) вентиляционные соединения могут включать в себя комбинации различных видов вентиляционных соединений.
| | | следующая лекция ==> | |
| Шахтные вентиляционные сети | | | Законы распределения воздуха в вентиляционных сетях |
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Параллельное соединение и его свойства
П араллельное соединение горных выработок может быть простым (рис.6.8) и сложным (рис.6.9).
араллельное соединение горных выработок может быть простым (рис.6.8) и сложным (рис.6.9).
Простым параллельным называется такое соединение вентиляционных ветвей, в котором все начала ветвей расходятся в одном узле, а сходятся в другом (рис.6.8).
Сложным параллельным соединением называется такое соединение, когда кроме параллельных ветвей расходящихся в одном узле и сходящимся в другом в этих ветвях имеются дополнительные параллельные ветви (рис.6.9).

Рис.6.9 Сложное параллельное соединение
Рассмотрим свойства простого параллельного соединения. Согласно определению депрессии разность давления в узлах 1, 2 определяет как депрессию любой ветви входящей в соединение, так и депрессию всего соединения, тогда можно записать
То есть в параллельном соединении депрессии всех ветвей одинаковы и равны депрессии всего соединения.
Так как к узлу 1 притекает поток Q , равный общему потоку соединения, а вытекают из него потоки q1, q2 qi qn , а в узле 2 все наоборот, то в соответствии с первым законом сетей можно записать
Q= 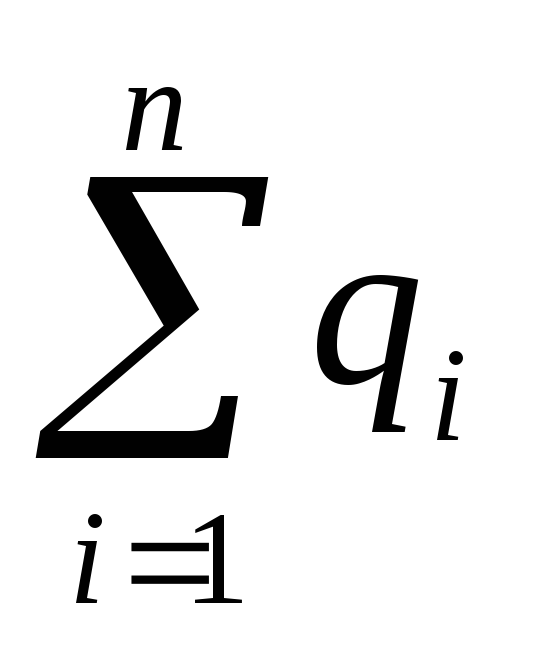 (6.26)
(6.26)
Общий поток параллельного соединения равен сумме потоков в отдельных ветвях.
Поток воздуха в любой ветви параллельного соединения, а также общий расход воздуха можно вы разить через депрессию и аэродинамическое сопротивление т. е.
Q= 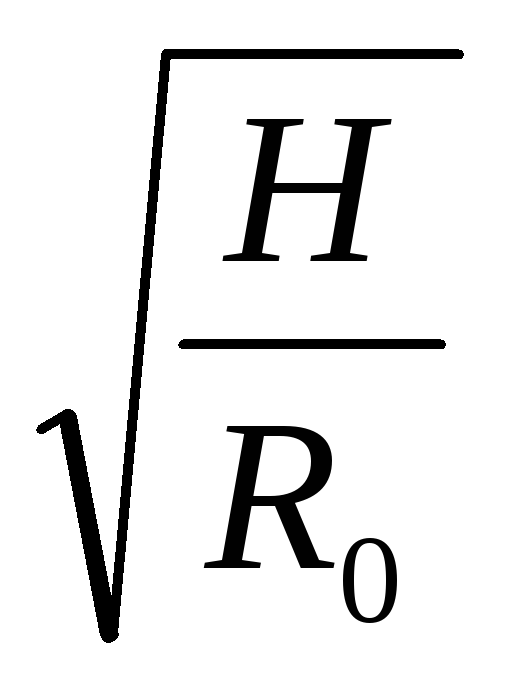 (6.27) qi=
(6.27) qi=  (6.28)
(6.28)
С учетом равенств (6.27), (6.28) равенство (6.26) можно записать в виде
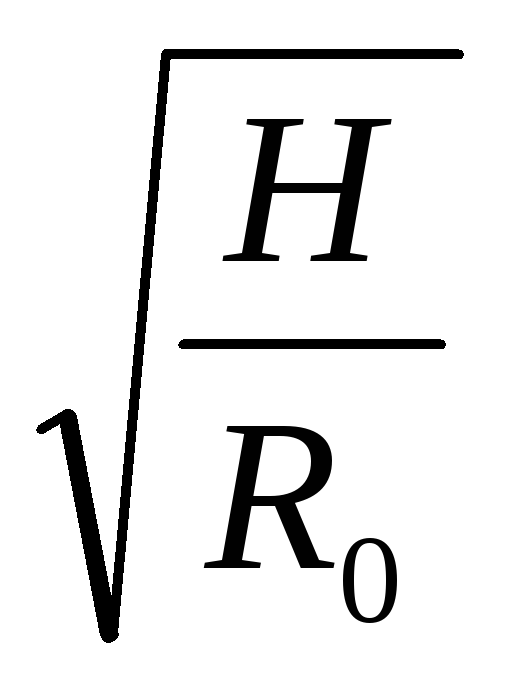 =
=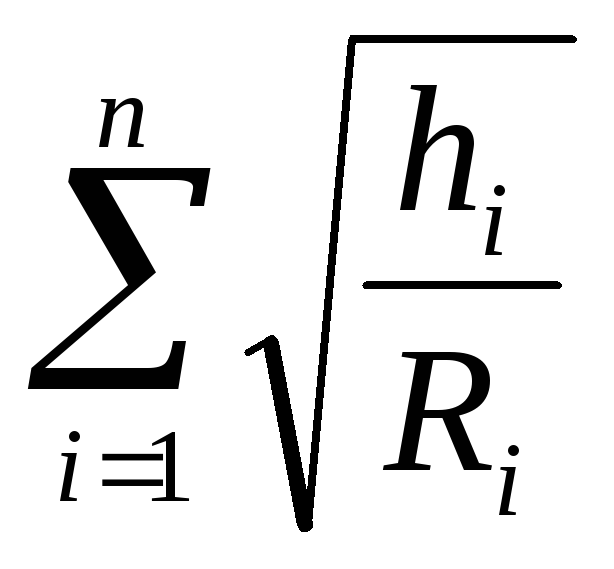 (6.29)
(6.29)
Так как в параллельном соединении Н=hi, то, сократив обе части последнего равенства на  , получим
, получим
 (6.30)
(6.30)
Величина обратная корню квадратному из сопротивления называется пропускной способностью, следовательно
K=  (6.31)
(6.31)
То есть общая пропускная способность параллельного соединения равна сумме пропускных способностей ветвей соединения.
Так как К=1/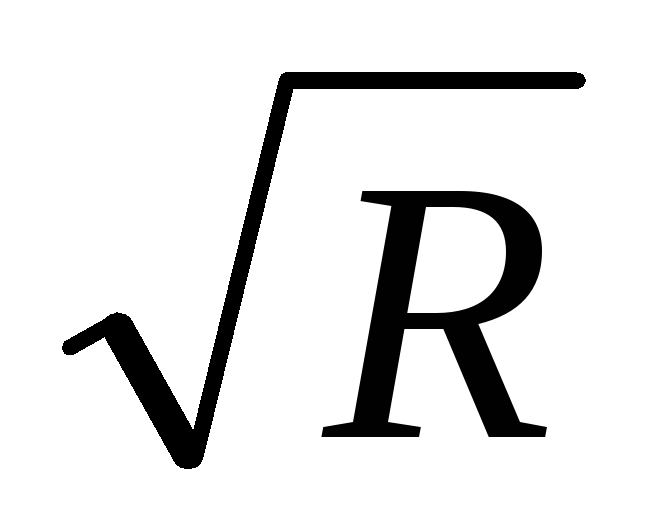 , то равенства (6.27), (6.28) можно переписать в виде
, то равенства (6.27), (6.28) можно переписать в виде
Q=K 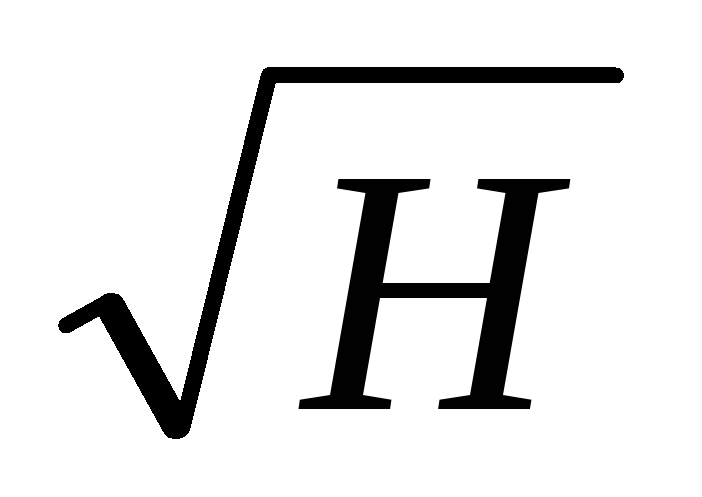 (6.32) qi=ki
(6.32) qi=ki  (6.33)
(6.33)
Так как в параллельном соединении H=hi то из равенств (6.32) (6.33) получим,
Qi= 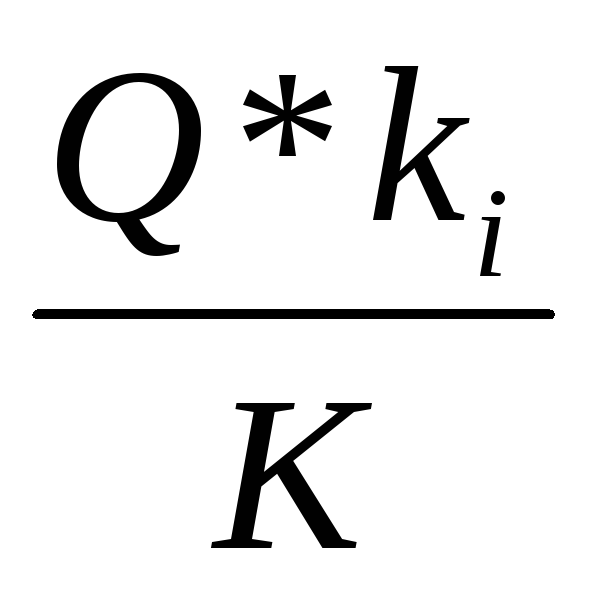 (6.34)
(6.34)
Потоки воздуха в отдельных ветвях параллельного соединения пропорциональны пропускной способности этих ветвей.
Теперь целесообразно выписать основные расчетные формулы последовательного и параллельного соединения и сравнить их.
 Н
Н
Q=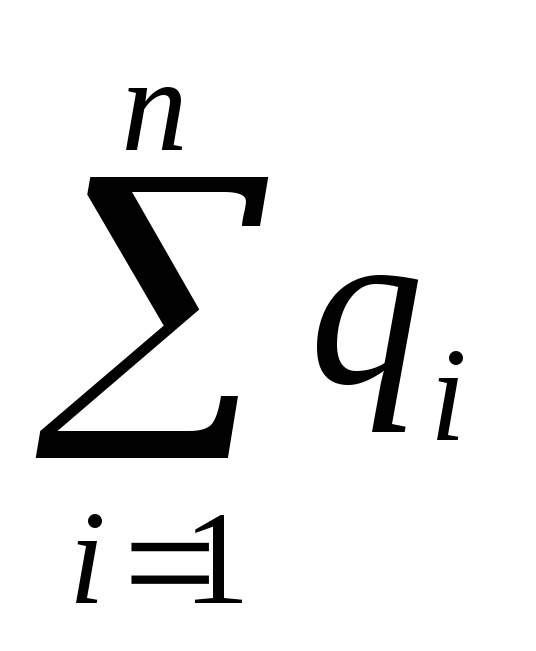

K=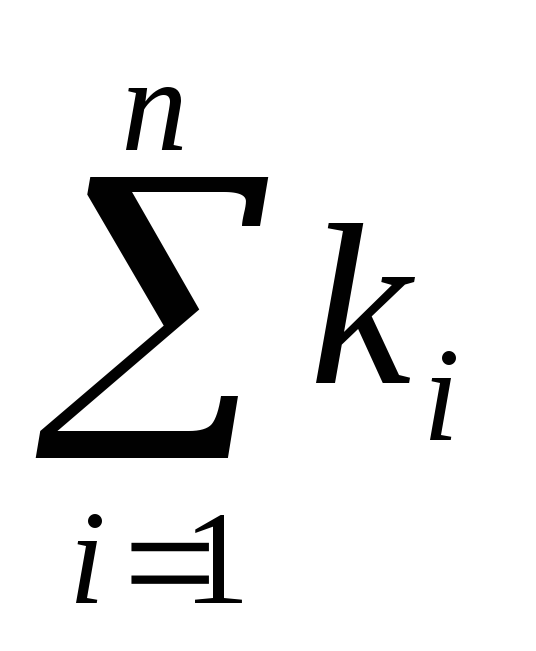
Hi =
Qi=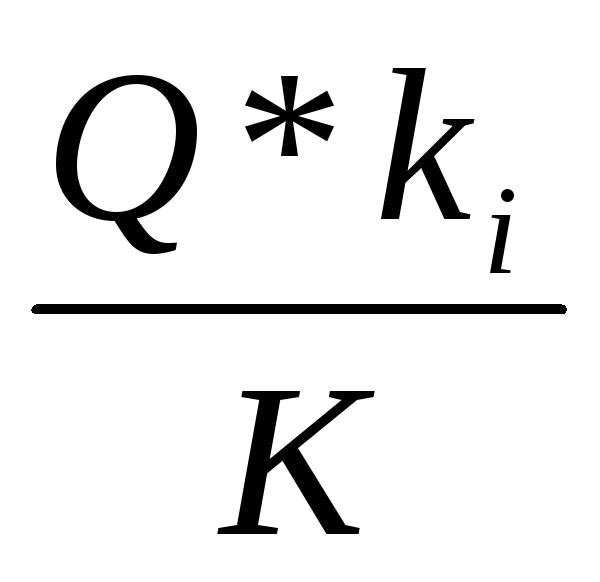
В последовательном соединении потоки воздуха во всех ветвях одинаковы, депрессия и сопротивления складываются, а депрессия каждой ветви пропорциональна ее сопротивлению.
В параллельном соединении депрессии всех ветвей одинаковы, потоки воздуха и пропускные способности суммируются, а расходы воздуха в ветвях пропорциональны их пропускной способности.
Полученные зависимости позволяют выполнять расчет сложных последовательно-параллельных соединений. Рассмотрим пример расчета сложного последовательно-параллельного соединения.
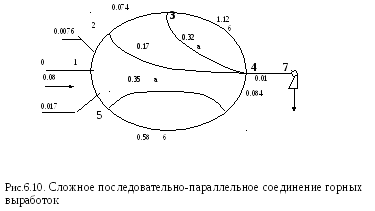
Заданы аэродинамические сопротивления ветвей сложного последовательно-параллельного соединения горных выработок и общая депрессия соединения (Рис.6.10). Рассчитать режим проветривания всех ветвей соединения (q, м 3 /c, h, даПа). Сопротивления ветвей на схеме заданы в киломюргах (кг*с 2 /м 8 ) , а депрессия в даПа.
Схема вентиляционных соединений и исходные данные для расчетов.
Решение задачи производится в следующей последовательности:
1. Обозначим узлы и ветви схемы представленной на рис.6.10. Если из одного узла в другой идет одна ветвь она обозначается числами-парами соединяемых узлов. Например, 0-1, 1-2, 6-4 и т. д. Отдельные ветви параллельных разветвлений обозначим номерами узлов и буквами. Например, 3-а-4, 3-б-4 и т. д. Разветвленный участок сети между двумя узлами номерами узлов в скобках. Например, (3-4) (5-6) и т. д.
2. Для определения общего расхода воздуха в сети Q и расхода воздуха в ветвях qi, необходимо определить общее сопротивление сети R0. Расчет величины R0 производим в следующей последовательности:
2.1 Определяем общее сопротивление простого параллельного соединения между узлами .3-4
R (3-4)= 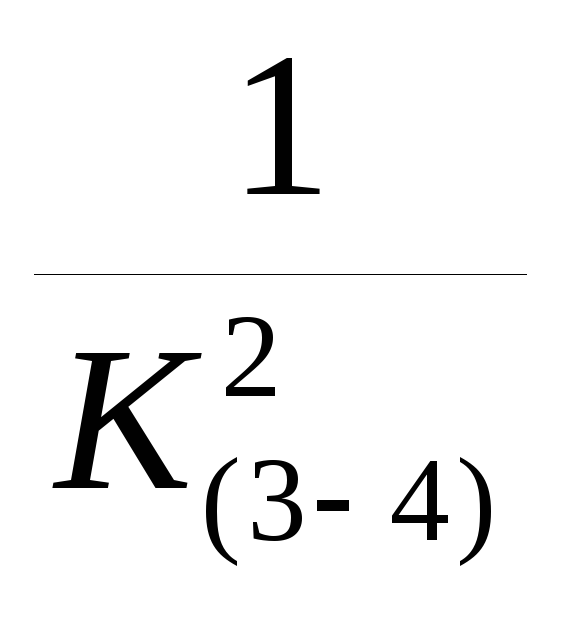 K (3-4)=
K (3-4)= +
+ 
2.2 Определяем общее сопротивление ветвей последовательного соединения
2.3 Определяем общее сопротивление параллельного соединения между узлами 2-4.
R (2-4)= 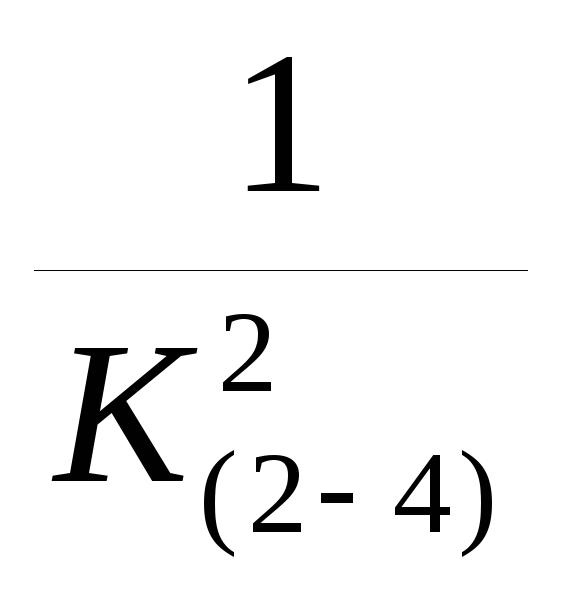 К(2-4)=
К(2-4)= +
+ 
2.4 Определяем общее сопротивление последовательного соединения ветвей 1-2 и (2-4)
2.5 Определяем общее сопротивление параллельного соединения между узлами 5-6
R (5-6)=  K(5-6)=
K(5-6)=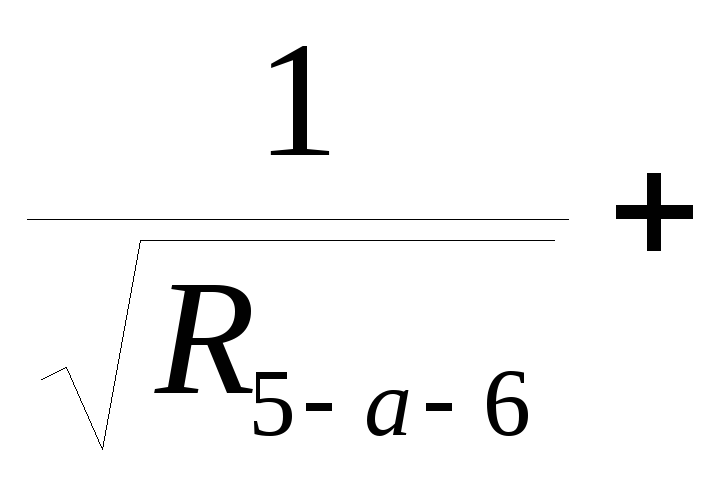
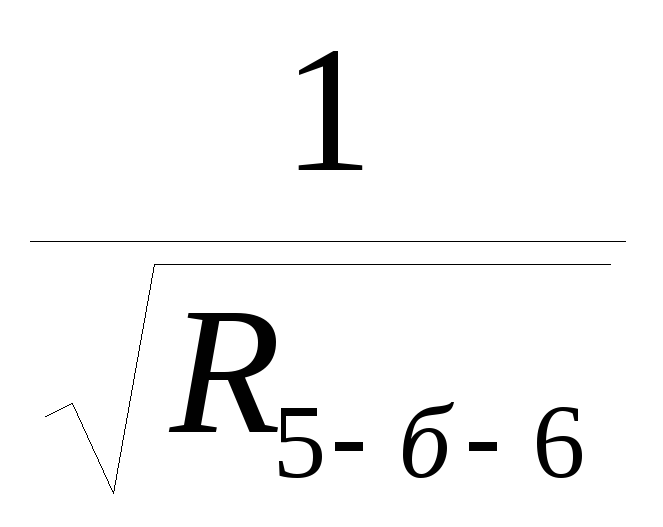
2.6 Определяем общее сопротивление последовательного соединения ветвей 1-5, (5-6) и 6-4
2.7 Определяем общее сопротивление параллельного соединения между узлами 1-4
R(1-4)=  K(1-4)=
K(1-4)=
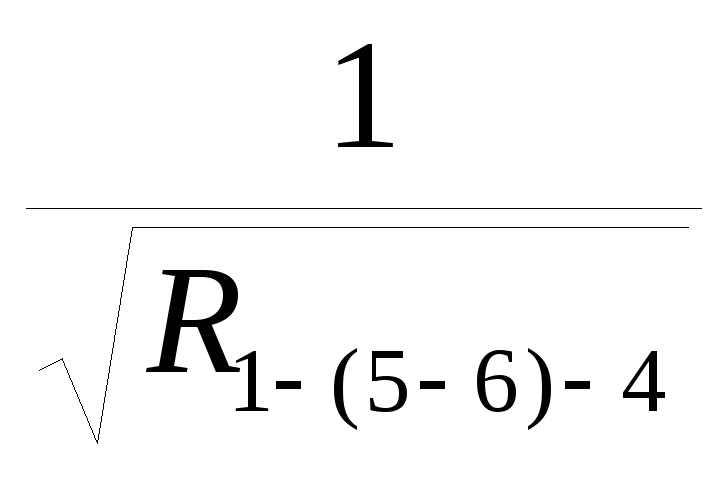
Определяем общее сопротивление вентиляционной сети
Определяем общий расход воздуха в сети
Q= 
3.1 Определяем расходы воздуха в ветвях параллельного соединения 1-(2-4) и
q1-(2-4)= 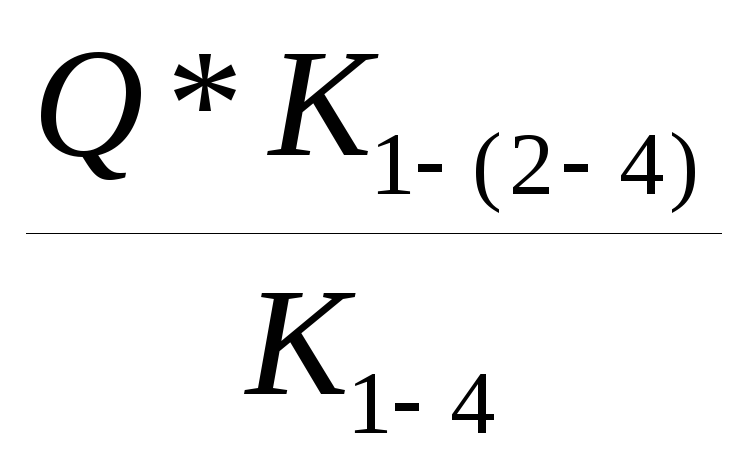 q1-(5-6)-4=
q1-(5-6)-4= 
3.2 Определяем расходы воздуха в ветвях параллельного соединения 2-(3-4) и 2-4
q (2-3)-4=  q 2-4=
q 2-4= 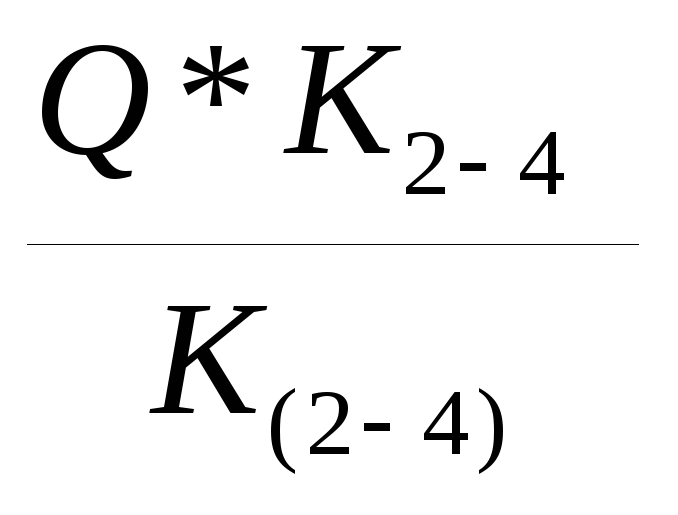
Определяем расходы воздуха в ветвях (3-а-4, и 3-б-4), по формулам
q3-а-4=  q 3-б-4=
q 3-б-4=

3.3 Определяем расходы воздуха в ветвях 5-а-6, (5-б-6) и (5-в-6), по формулам
q 5-а-6=  q (5-б-6)=
q (5-б-6)=

Результаты расчетов сложного последовательно-параллельного соединения, представленного на рис.6.10 по формулам сводим в таблицу.
Результаты расчетов воздухораспределения в сложном последовательно параллельном соединении




